Probabilistic Artificial Intelligence - Markov Chain Monte Carlo Methods

Markov Chain Monte Carlo Methods

The key idea of Markov chain Monte Carlo methods is to construct a Markov chain, which is efficient to simulate and has the stationary distribution p.

Markov Chains

Intuitively, the Markov property states that future behavior is independent of past states given the present state.

Markov chains can be classified into different types based on their behavior. These classifications include time-homogeneous and time-inhomogeneous Markov chains, irreducible Markov chains, and periodic and aperiodic Markov chains.

We restrict our attention to time-homogeneous Markov chains. That is, the transition probabilities do not change over time, which can be characterized by a transition function.

Irreducible Markov chains are those in which every state can be reached from any other state, while periodic Markov chains exhibit a repeating pattern in their states. On the other hand, aperiodic Markov chains do not exhibit any regular pattern in their states. If there is no fixed period at which the probabilities return to the starting values, the chain is classified as aperiodic. Aperiodic Markov chains often display a more complex and unpredictable behavior compared to periodic ones.

Stationarity

Convergence

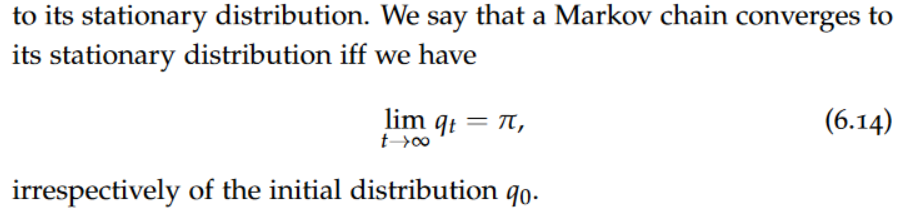
A Markov Chain is called ergodic, if there exists a finite t such that every state can be reached from every state in exactly t steps.

Fundamental theorem of ergodic Markov chains

Detailed Balance Equation

Ergodic Theorem

This result is the fundamental reason for why Markov chain Monte Carlo methods are possible. In practice, one observes that Markov chain Monte Carlo methods have a so-called “burn-in” time during which the distribution of the Markov chain does not yet approximate the posterior distribution well. Typically, the first t0 samples are therefore discarded. It is not clear in general how T and t0 should be chosen such that the estimator is unbiased, rather they have to be tuned.

Elementary Sampling Methods

Metropolis-Hastings Algorithm

Gibbs Sampling

A popular example of a Metropolis-Hastings algorithm is Gibbs sampling.

Intuitively, by re-sampling single coordinates according to the posterior distribution given the other coordinates, Gibbs sampling finds states that are successively “more” likely.

Langevin Dynamics

Gibbs Distributions

references

https://www.collimator.ai/reference-guides/what-is-a-aperiodic-markov-chain