pai - active learning

Active learning

Active learning is a machine learning paradigm in which a model is trained on a dataset that is not entirely labeled. Instead of relying solely on a fully labeled dataset for training, active learning involves an iterative process where the model actively selects the most informative instances from an unlabeled pool, queries an oracle (typically a human annotator), and adds the newly labeled instances to the training set. The model is then retrained on the expanded labeled dataset.

The key idea behind active learning is to strategically choose the most valuable instances for labeling, with the goal of improving the model’s performance while minimizing the number of labeled instances needed. This process is especially beneficial when obtaining labeled data is expensive or time-consuming.

Active learning strategies vary in how they select instances for labeling. Common strategies include uncertainty sampling (select instances where the model is uncertain), query-by-committee (select instances where different model hypotheses disagree), and diversity sampling (select instances to ensure diverse coverage of the input space).

Conditional Entropy

Intuitively, the conditional entropy of X given Y describes our average surprise about realizations of X given a particular realization of Y, averaged over all such possible realizations of Y. In other words, conditional entropy corresponds to the expected remaining uncertainty in X after we observe Y.

That is, the joint entropy of X and Y is given by the uncertainty about X and the additional uncertainty about Y given X.

Mutual Information

In words, we subtract the uncertainty left about X after observing Y from our initial uncertainty about X. This measures the reduction in our uncertainty in X (as measured by entropy) upon observing Y.

Thus, the mutual information between X and Y can be understood as the approximation error (or information loss) when assuming that X and Y are independent.

Thus, the conditional mutual information corresponds to the reduction of uncertainty in X when observing Y, given we already observed Z.

Following our introduction of mutual information, it is natural to answer the question “where should I collect data?” by saying “wherever mutual information is maximized”.

Submodularity of Mutual Information

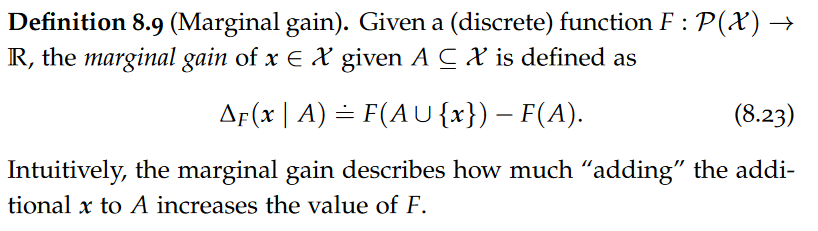
That is, “adding” x to the smaller set A yields more marginal gain than adding x to the larger set B. In other words, the function F has “diminishing returns”. In this way, submodularity can be interpreted as a notion of “concavity” for discrete functions.

Maximizing Mutual Information

Uncertainty Sampling

Therefore, if f is modeled by a Gaussian and we assume homoscedastic noise, greedily maximizing mutual information corresponds to simply picking the point x with the largest variance. This strategy is also called uncertainty sampling.

Heteroscedastic Noise

Uncertainty sampling is clearly problematic if the noise is heteroscedastic. If there are a particular set of inputs with a large aleatoric uncertainty dominating the epistemic uncertainty, uncertainty sampling will continuously choose those points even though the epistemic uncertainty will not be reduced substantially.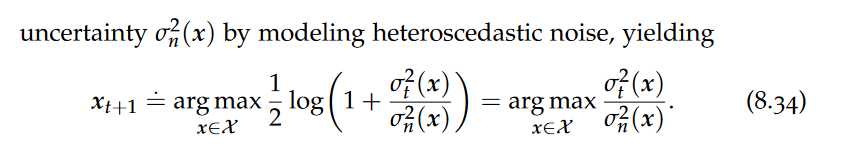

Thus, we choose locations that trade large epistemic uncertainty with large aleatoric uncertainty. Ideally, we find a location where the epistemic uncertainty is large, and the aleatoric uncertainty is low, which promises a significant reduction of uncertainty around this location.

Classification

Here, uncertainty sampling corresponds to selecting samples that maximize the entropy of the predicted label yx.