pai - Markov Decision Processes

Markov Decision Processes

Planning deals with the problem of deciding which action an agent should play in a (stochastic) environment(An environment is stochastic as opposed to deterministic, when the outcome of actions is random.). A key formalism for probabilistic plan ning in known environments are so-called Markov decision processes.

Our fundamental objective is to learn how the agent should behave to optimize its reward. In other words, given its current state, the agent should decide (optimally) on the action to play. Such a decision map — whether optimal or not — is called a policy.

For the purpose of our discussion of Markov decision processes and reinforcement learning, we will focus on a very common reward called discounted payoff.

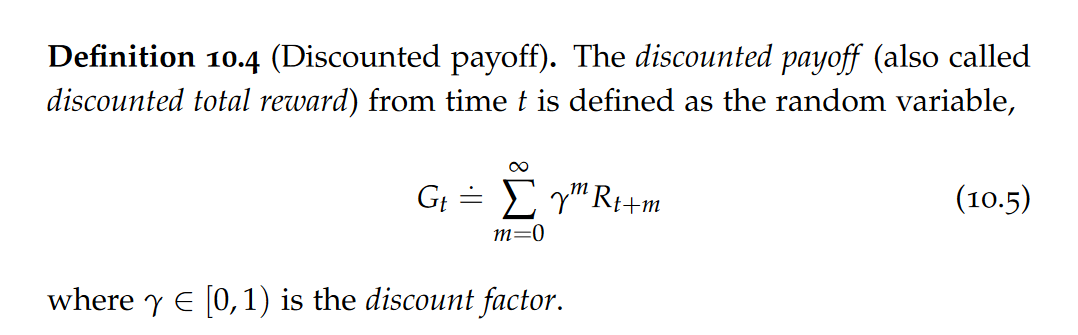
Because we assumed stationary dynamics, rewards, and policies, the discounted payoff starting from a given state x will be independent of the start time t.

Bellman Expectation Equation

Let us now see how we can compute the value function：

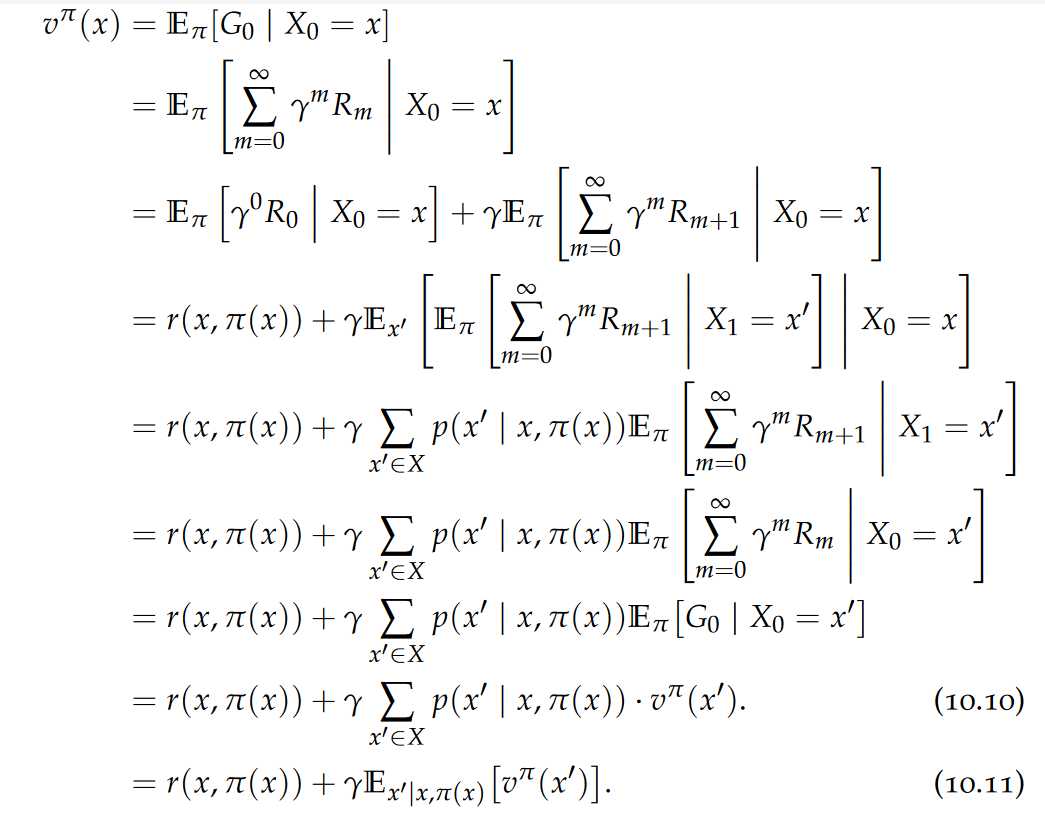
This equation is known as the Bellman expectation equation, and it shows a recursive dependence of the value function on itself. The intuition is clear: the value of the current state corresponds to the reward from the next action plus the discounted sum of all future rewards obtained from the subsequent states.

Policy Evaluation

Bellman’s expectation equation tells us how we can find the value function vπ of a fixed policy π using a system of linear equations.

Fixed-point Iteration

Policy Optimization

Greedy Policies

Bellman Optimality Equation

These equations are also called the Bellman optimality equations. Intuitively, the Bellman optimality equations express that the value of a state under an optimal policy must equal the expected return for the best action from that state. Bellman’s theorem is also known as Bellman’s optimality principle, which is a more general concept.

Policy Iteration

It can be shown that policy iteration converges to an exact solution in a polynomial number of iterations.Each iteration of policy iteration requires computing the value function, which we have seen to be of cubic complexity in the number of states.

Value Iteration

Value iteration converges to an ε-optimal solution in a polynomial number of iterations. Unlike policy iteration, value iteration does not converge to an exact solution in general.an iteration of 7 Sparsity refers to the interconnectivity of the state space. When only few states are reachable from any state, we call an MDP sparse. value iteration can be performed in (virtually) constant time in sparse Markov decision processes.

Partial Observability

In this section, we consider how Markov decision processes can be extended to a partially observable setting where the agent can only access noisy observations Yt of its state Xt.

Observe that a Kalman filter can be viewed as a hidden Markov model with conditional linear Gaussian motion and sensor models and a Gaussian prior on the initial state.

POMDPs can be reduced to a Markov decision process with an enlarged state space.