pai - Tabular Reinforcement Learning
Tabular Reinforcement Learning
The Reinforcement Learning Problem
Reinforcement learning is concerned with probabilistic planning in unknown environments. In this chapter, we will begin by considering reinforcement learning with small state and action spaces. This setting is often called the tabular setting, as the value functions can be computed exhaustively for all states and stored in a table.
Clearly, the agent needs to trade exploring and learning about the environment with exploiting its knowledge to maximize rewards. In fact, Bayesian optimization can be viewed as reinforcement learning with a fixed state and a continuous action space: In each round, the agent plays an action, aiming to find the action that maximizes the reward.Another key challenge of reinforcement learning is that the observed data is dependent on the played actions.
Trajectories

Crucially, the newly observed states xt+1 and the rewards rt (across multiple transitions) are conditionally independent given the previous states xt and actions at. This independence property is crucial for being able to learn about the underlying Markov decision process. Notably, this implies that we can apply the law of large numbers (1.83) and Hoeffding’s inequality (1.87) to our estimators of both quantities.
The collection of data is commonly classified into two settings. In the episodic setting, the agent performs a sequence of “training” rounds (called episodes). In the beginning of each round, the agent is reset to some initial state. In contrast, in the continuous setting (or non-episodic,or online setting), the agent learns online.
control
Another important distinction in how data is collected, is the distinction between on-policy and off-policy control. As the names suggest, on-policy methods are used when the agent has control over its own actions, in other words, the agent can freely choose to follow any policy. In contrast, off-policy methods can be used even when the agent cannot freely choose its actions. Off-policy methods are therefore able to make use of observational data.Off-policy methods are therefore more sample-efficient than on-policy methods. This is crucial, especially in settings where conducting experiments (i.e., collecting new data) is expensive.
On-Policy learning algorithms are the algorithms that evaluate and improve the same policy which is being used to select actions. Off-Policy learning algorithms evaluate and improve a policy that is different from Policy that is used for action selection.
To understand the difference between on-policy learning and off-policy learning one must first understand the difference between the behavior policy (i.e., sampling policy) and the update policy. The behavior policy is the policy an agent follows when choosing which action to take in the environment at each time step. The update policy is how the agent updates the Q-function. On-policy algorithms attempt to improve upon the current behavior policy that is used to make decisions and therefore these algorithms learn the value of the policy carried out by the agent, Off-policy algorithms learn the value of the optimal policy and can improve upon a policy that is different from the behavior policy. Determining if the update and behavior policy are the same or different can give us insight into whether or not the algorithm is on-policy or off-policy.
Model-based Approaches
Approaches to reinforcement learning are largely categorized into two classes. Model-based approaches aim to learn the underlying Markov decision process. In contrast, model-free approaches learn the value function directly.
Learning the Underlying Markov Decision Process
A natural first idea is to use maximum likelihood estimation to approximate transition and reward function.

ε-greedy Algorithm

The key problem of ε-greedy is that it explores the state space in an uninformed manner. In other words, it explores ignoring all past experience. It thus does not eliminate clearly suboptimal actions.
Rmax Algorithm
A key principle in effectively trading exploration and exploitation is “optimism in the face of uncertainty”. Let us apply this principle to the reinforcement learning setting. The key idea is to assume that the dynamics and rewards model “work in our favor” until we have learned “good estimates” of the true dynamics and rewards.

How many transitions are “enough”? We can use Hoeffding’s inequality to get a rough idea!

challenges
Model-free Approaches
A significant benefit to model-based reinforcement learning is that it is inherently off-policy. That is, any trajectory regardless of the policy used to obtain it can be used to improve the model of the underlying Markov decision process. In the model-free setting, this not necessarily true.
On-policy Value Estimation

Note that to estimate this expectation we use a single(!) sample.However, there is one significant problem in this approximation. Our approximation of vπ does in turn depend on the (unknown) true value of vπ. The key idea is to use a bootstrapping estimate of the value function instead. That is, in place of the true value function vπ, we will use a “running estimate” Vπ. In other words, whenever observing a new transition, we use our previous best estimate of vπ to obtain a new estimate Vπ.
Crucially, using a bootstrapping estimate generally results in biased estimates of the value function. Moreover, due to relying on a single sample, the estimates tend to have very large variance.
TD-learning
The variance of the estimate is typically reduced by mixing new estimates of the value function with previous estimates using a learning rate αt. This yields the temporal-difference learning algorithm.

TD-learning is a fundamentally on-policy method. That is, for the estimates Vπ to converge to the true value function vπ, the transitions that are used for the estimation must follow policy π.
SARSA

Off-policy Value Estimation

This adapted update rule explicitly chooses the subsequent action a′ according to policy π whereas SARSA absorbs this choice into the Monte Carlo approximation. The algorithm has analogous convergence guarantees to those of SARSA. Crucially, this algorithm is off-policy. As noted, the key difference to the on-policy TD-learning and SARSA is that our estimate of the Qfunction explicitly keeps track of the next-performed action. It does so for any action in any state.
Q-learning
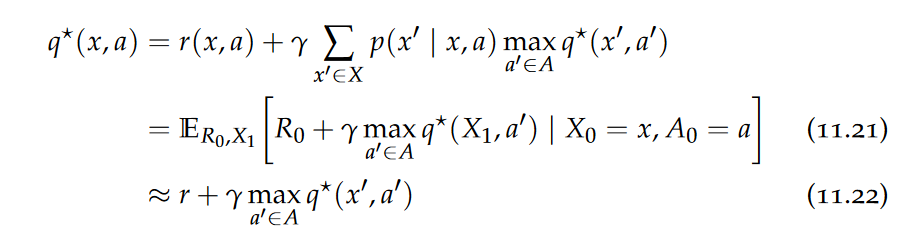
Crucially, the Monte Carlo approximation of eq. (11.21) does not depend on the policy. Thus, Q-learning is an off-policy method.
Optimistic Q-learning

Challenges
We have seen that both the model-based Rmax algorithm and the modelfree Q-learning take time polynomial in the number of states |X| and the number of actions |A| to converge. While this is acceptable in small grid worlds, this is completely unacceptable for large state and action spaces.
references
pai - Tabular Reinforcement Learning
install_url to use ShareThis. Please set it in _config.yml.