pai - Model-free Approximate Reinforcement Learning

Model-free Approximate Reinforcement Learning

Tabular Reinforcement Learning as Optimization

In particular, in the tabular setting (i.e., over a discrete domain), we can parameterize the value function exactly by learning a separate parameter for each state.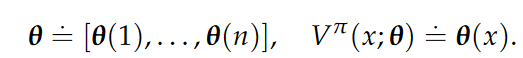

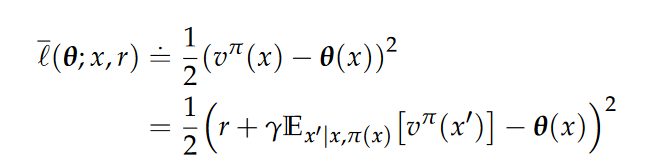
Now, we cannot compute this derivative because we cannot compute the expectation. Firstly, the expectation is over the true value function which is unknown to us. Secondly, the expectation is over the transition model which we are trying to avoid in model-free methods. To resolve the first issue, analogously to TD-learning, instead of learning the true value function vπ which is unknown, we learn the bootstrapping estimate Vπ. To resolve the first issue, analogously to TD-learning, instead of learning the true value function vπ which is unknown, we learn the bootstrapping estimate Vπ. we will use a Monte Carlo estimate using a single sample. Recall that this is only possible because the transitions are conditionally independent given the state-action pair.

Therefore, TD-learning is essentially performing stochastic gradient descent using the TD-error as an unbiased gradient estimate.
Stochastic gradient descent with a bootstrapping estimate is also called stochastic semi-gradient descent.

Value Function Approximation

Our goal for large state-action spaces is to exploit the smoothness properties5 of the value function to condense the representation.

Heuristics

The vanilla stochastic semi-gradient descent is very slow.
There are mainly two problems.
As we are trying to learn an approximate value function that depends on the bootstrapping estimate, this means that the optimization target is “moving” between iterations. In practice, moving targets lead to stability issues. One such technique aiming to “stabilize” the optimization targets is called neural fitted Q-iteration or deep Q-networks (DQN). DQN updates the neural network used for the approximate bootstrapping estimate infrequently to maintain a constant optimization target across multiple episodes. One approach is to clone the neural network and maintain one changing neural network (“online network”) for the most recent estimate of the Q-function which is parameterized by θ, and one fixed neural network (“target network”) used as the target which is parameterized by θold and which is updated infrequently.

This technique is known as experience replay. Another approach is Polyak averaging where the target network is gradually “nudged” by the neural network used to estimate the Q function.

Now, observe that the estimates Q⋆ are noisy estimates of q⋆. The fact that the update rules can be affected by inaccuracies (i.e., noise in the estimates) of the learned Q-function is known as the “maximization bias”. Double DQN (DDQN) is an algorithm that addresses this maximization bias. Instead of picking the optimal action with respect to the old network, it picks the optimal action with respect to the new network. Intuitively, this change ensures that the evaluation of the target network is consistent with the updated Q-function, which makes it more difficult for the algorithm to be affected by noise.

Policy Approximation

Methods that find an approximate policy are also called policy search methods or policy gradient methods. Policy gradient methods use randomized policies for encouraging exploration.

Estimating Policy Values

The policy value function measures the expected discounted payoff of policy π.

Reinforce Gradient

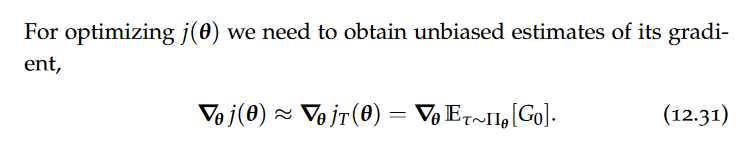
In this context, however, we cannot apply the reparameterization trick. Fortunately, there is another way of estimating this gradient.

When using a neural network for the parameterization of the policy π, we can use automatic differentiation to obtain unbiased gradient estimates. However, it turns out that the variance of these estimates is very large. Using so-called baselines can reduce the variance dramatically.

The baseline essentially captures the expected or average value, providing a reference point. By subtracting this reference point, the updates become more focused on the deviations from the expected values, which can reduce the variance in these deviations.

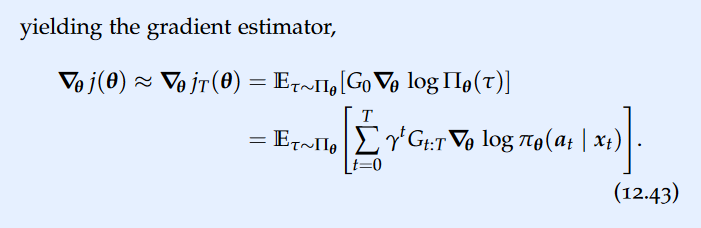
Typically, policy gradient methods are slow due to the large variance in the score gradient estimates. Because of this, they need to take small steps and require many rollouts of a Markov chain. Moreover, we cannot reuse data from previous rollouts, as policy gradient methods are fundamentally on-policy.

Actor-Critic Methods

Actor-Critic methods reduce the variance of policy gradient estimates by using ideas from value function approximation. They use function approximation both to approximate value functions and to approximate policies.

Advantage Function

Intuitively, the advantage function is a shifted version of the state-action function q that is relative to 0. It turns out that using this quantity instead, has numerical advantages.

Policy Gradient Theorem

Intuitively, ρθ(x) measures how often we visit state x when following policy πθ. It can be thought of as a “discounted frequency”. Importantly, ρθ is not a probability distribution, as it is not normalized to integrate to 1. Instead, ρθ is what is often called a finite measure. Therefore, eq. (12.57) is not a real expectation!

On-policy Actor-Critics

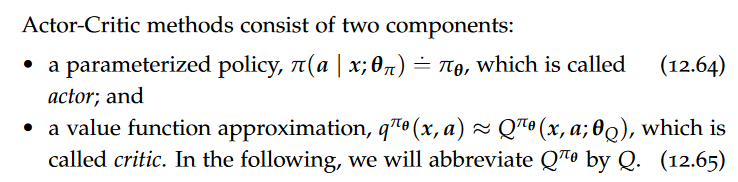
OAC

Due to the use of TD-learning for learning the critic, this algorithm is fundamentally on-policy.

A2C

that the Q-function is an absolute quantity, whereas the advantage function is a relative quantity, where the sign is informative for the gradient direction. Intuitively, an absolute value is harder to estimate than the sign. Actor-Critic methods are therefore often implemented with respect to the advantage function rather than the Q-function.

GAE/GAAE

Taking a step back, observe that the policy gradient methods such as REINFORCE generally have high variance in their gradient estimates. However, due to using Monte Carlo estimates of Gt, the gradient estimates are unbiased. In contrast, using a bootstrapped Q-function to obtain gradient estimates yields estimates with a smaller variance, but those estimates are biased. We are therefore faced with a bias-variance tradeoff. A natural approach is therefore to blend both gradient estimates to allow for effectively trading bias and variance. This leads to algorithms such as generalized advantage estimation (GAE/GAAE).

Improving sample efficiency(TRPO/PPO)

Actor-Critic methods generally suffer from low sample efficiency. One well-known variant that slightly improves the sample efficiency is trust-region policy optimization (TRPO).

Intuitively, taking the expectation with respect to the previous policy πθk , means that we can reuse data from rollouts within the same iteration. TRPO allows reusing past data as long as it can still be “trusted”. This makes TRPO “somewhat” off-policy. Fundamentally, though, TRPO is still an on-policy method. Proximal policy optimization (PPO) is a heuristic variant of TRPO that often works well in practice.

Off-policy Actor-Critics

These algorithms use the reparameterization gradient estimates, instead of score gradient estimators.

DDPG

As our method is off-policy, a simple idea in continuous action spaces is to add Gaussian noise to the action selected by πθ — also known as Gaussian noise “dithering”. This corresponds to an algorithm called deep deterministic policy gradients.
This algorithm is essentially equivalent to Q-learning with function approximation (e.g., DQN), with the only exception that we replace the maximization over actions with the learned policy πθ.

Twin delayed DDPG (TD3) is an extension of DDPG that uses two separate critic networks for predicting the maximum action and evaluating the policy. This addresses the maximization bias akin to Double-DQN. TD3 also applies delayed updates to the actor network, which increases stability.

Off-Policy Actor Critics with Randomized Policies

The algorithm that uses eq. (12.81) to obtain gradients for the critic and reparameterization gradients for the actor is called stochastic value gradients (SVG).

Off-policy Actor-Critics with Entropy Regularization

In practice, algorithms like SVG often do not explore enough. A key issue with relying on randomized policies for exploration is that they might collapse to deterministic policies.

A simple trick that encourages a little bit of extra exploration is to regularize the randomized policies “away” from putting all mass on a single action. This approach is known as entropy regularization and it leads to an analogue of Markov decision processes called entropy-regularized Markov decision process, where suitably defined regularized state-action value functions (so-called soft value functions) are used.

soft actor critic(SAC)

references

https://towardsdatascience.com/soft-actor-critic-demystified-b8427df61665
https://github.com/tsmatz/reinforcement-learning-tutorials/blob/master/06-sac.ipynb
https://spinningup.openai.com/en/latest/algorithms/sac.html
https://towardsdatascience.com/policy-gradients-in-a-nutshell-8b72f9743c5d
https://lilianweng.github.io/posts/2018-04-08-policy-gradient/